戴维南定理的定义与应用

戴维南定理攻略：解密定义与应用

1. 什么是戴维南定理？

戴维南定理是一种数学定理，用来解释一个几何学中的基本概念。它描述了一个三角形内部的点连接三个顶点构成的三条线段，在特定条件下的关系。该定理常用于证明三角形的各种性质，包括相似性、垂直性等。

2. 戴维南定理的核心观点

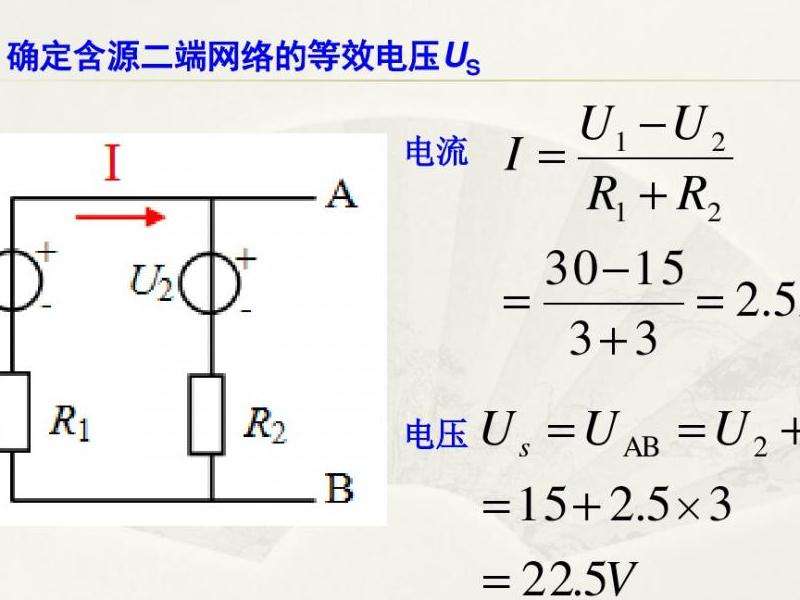
戴维南定理的核心思想是：如果在三角形ABC内部取一点P，分别连接AP、BP、CP并延长交边BC、AC、AB于L、M、N，则有以下等式成立：

（BL/CL）*（CM/AM）*（AN/BN）=1

其中BL、CL、CM、AM、AN、BN是线段长度。

3. 戴维南定理的应用

戴维南定理可以应用在不同的几何问题中，其中一些应用包括：

3.1 证明三角形相似

通过戴维南定理，可以证明两个三角形相似。如果在两个三角形内部取点P和Q，并满足戴维南定理的条件，那么这两个三角形是相似的。

3.2 求解三角形内部点的位置

在给定三角形ABC和戴维南定理的条件下，可以通过解方程组来确定点P的具体位置坐标。这对于一些几何问题的解决具有重要意义。

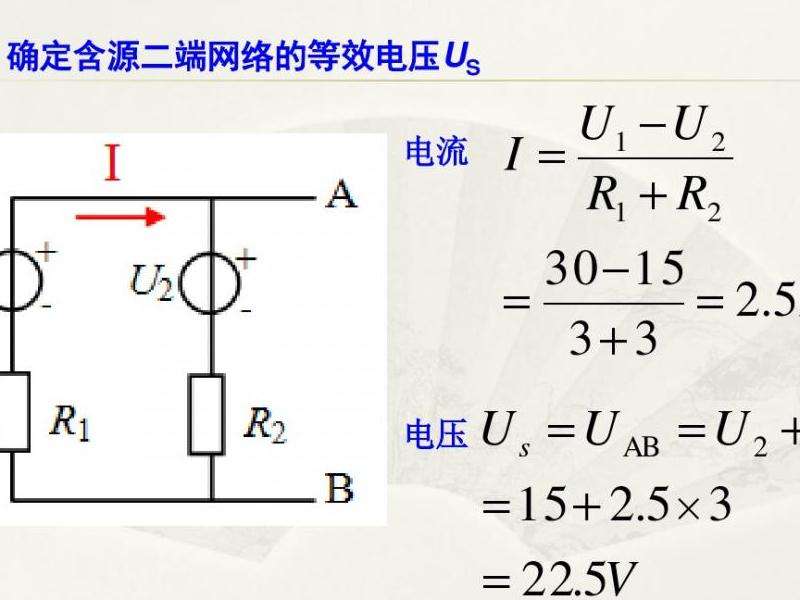
3.3 证明垂直性

戴维南定理也可以用来证明三条线段的垂直性。如果在三角形内部取一点P，并且满足戴维南定理条件，那么可以通过结合垂直性的性质来证明线段的垂直关系。

4. 总结

戴维南定理是数学中一个重要的几何概念，通过理解其定义和应用，我们可以更好地解决各种与三角形相关的问题。不仅如此，戴维南定理也是训练逻辑思维和解决问题能力的好工具。

通过本篇攻略，希望读者能够更加深入地理解戴维南定理的定义与应用，同时也能够灵活运用该定理解决数学问题。祝大家在数学的海洋中探索出更多的乐趣！

Tags：

转载：感谢您对电子工程网_电子行业技术最新资讯网站平台的认可，以及对我们原创作品以及文章的青睐，非常欢迎各位朋友分享到个人站长或者朋友圈，但转载请说明文章出处“来源演示站”。/yingyong/536.html

很赞哦！ ()